sandro's blog

Solving Markov Decision Processes Using Linear Programming

  • Feb 09, 2025

This post presents a solution to a Markov Decision Process (MDP) problem using linear programming (LP). We explore a recycling robot problem that optimizes actions to collect soda cans while managing battery levels. The approach is based on Bellman optimality equations and implemented in Python using the cvxpy library.

View Project on GitHub

Introduction

This document presents a solution to a Markov Decision Process (MDP) problem using linear programming (LP). The problem, as proposed by Sutton and Barto, involves optimizing the actions of a robot that collects soda cans while managing its battery levels efficiently.

Problem Statement

The robot operates in two battery states: high and low. Depending on the state, the robot can choose among several actions:

  • Search for cans: Yields an expected reward of 2, but in the high state, it risks transitioning to the low state with probability 1 - α. In the low state, searching risks running out of battery, penalized by -3 (after which the battery is set to high state).
  • Wait for cans: Provides an expected reward of 1 and keeps the battery state unchanged.
  • Charge the battery: Available only in the low state, it transitions to the high state without a direct reward.

The objective is to maximize the cumulative discounted reward with a discount factor γ = 0.9.

Mathematical Formulation

Using the Bellman optimality equations, the problem is formulated as an LP. Let $v(h)$ and $v(l)$ represent the value functions for the high and low battery states, respectively. The rewards are defined as $r_{\text{search}} = 2$ and $r_{\text{wait}} = 1$. The constraints are derived as follows:

High state (h): \(v(h) \geq r_{\text{wait}} + \gamma \cdot v(h)\) \(v(h) \geq r_{\text{search}} + \gamma \cdot (\alpha \cdot v(h) + (1 - \alpha) \cdot v(l))\)

Low state (l): \(v(l) \geq r_{\text{wait}} + \gamma \cdot v(l)\) \(v(l) \geq \gamma \cdot v(h)\) \(v(l) \geq \beta \cdot r_{\text{search}} - 3 \cdot (1 - \beta) + \gamma \cdot ((1 - \beta) \cdot v(h) + \beta \cdot v(l))\)

The LP formulation is: Minimize: $v(h)$ (or $v(h) + v(l)$) Subject to: the above constraints.

Python Implementation

The following Python code uses the cvxpy library to solve the linear programming formulation of the recycling robot problem:

import cvxpy as cp

def recycling_robot(alpha, beta, r_s=2, r_w=1, gamma=0.9):
    # Decision variables
    v_h = cp.Variable(name="v_h")  # Value for high state
    v_l = cp.Variable(name="v_l")  # Value for low state

    # Objective
    objective = cp.Minimize(v_h)  # we can also use v_h + v_l

    # Constraints (Bellman)
    constraints = [
        # high -> wait
        v_h >= r_w + gamma * v_h,

        # high -> search
        v_h >= r_s + gamma * (alpha * v_h + (1 - alpha) * v_l),

        # low -> wait
        v_l >= r_w + gamma * v_l,

        # low -> recharge
        v_l >= gamma * v_h,

        # low -> search
        v_l >= beta * r_s - 3 * (1 - beta) + gamma * ((1 - beta) * v_h + beta * v_l)
    ]

    # Solve the problem using a linear programming solver
    # Ensure GLPK or another suitable LP solver is installed.
    # Other options: cp.ECOS, cp.SCS (though GLPK is good for pure LPs)
    prob = cp.Problem(objective, constraints)
    prob.solve(solver=cp.GLPK) 

    # Check if the problem was solved successfully
    if prob.status not in ["optimal", "optimal_inaccurate"]:
        print(f"Problem not solved optimally. Status: {prob.status}")
        return {
            "v_h": None, "v_l": None,
            "pi_h": None, "pi_l": None,
            "status": prob.status
        }

    # Convert v_h and v_l to float
    v_h_val = float(v_h.value)
    v_l_val = float(v_l.value)

    # Calculate optimal policies
    pi_h = -1 # Undetermined
    pi_l = -1 # Undetermined

    eps = 1e-5 # A small epsilon for float comparisons

    # Determine policy for high state
    if abs(v_h_val - (r_w + gamma * v_h_val)) < eps:
        pi_h = "wait"
    elif abs(v_h_val - (r_s + gamma * (alpha * v_h_val + (1 - alpha) * v_l_val))) < eps:
        pi_h = "search"

    # Determine policy for low state
    if abs(v_l_val - (r_w + gamma * v_l_val)) < eps:
        pi_l = "wait"
    elif abs(v_l_val - (gamma * v_h_val)) < eps:
        pi_l = "recharge"
    elif abs(v_l_val - (beta * r_s - 3 * (1 - beta) + gamma * ((1 - beta) * v_h_val + beta * v_l_val))) < eps:
        pi_l = "search"
    
    # Fallback if multiple conditions are met (due to floating point issues or multiple optimal actions)
    # This simple check might need refinement for robust policy extraction if multiple actions are truly optimal.
    # For now, it picks the first one that matches.

    return {
        "v_h": v_h_val,
        "v_l": v_l_val,
        "pi_h": pi_h,
        "pi_l": pi_l,
    }

Results and Discussion

The approach presented successfully solves the recycling robot problem using Python. The results illustrate the optimal value functions and policies for 𝛼 ∈ ( 0 , 1 ) α∈(0,1) and 𝛽 ∈ ( 0 , 1 ) β∈(0,1) , demonstrating how MDPs can be effectively solved using LP.

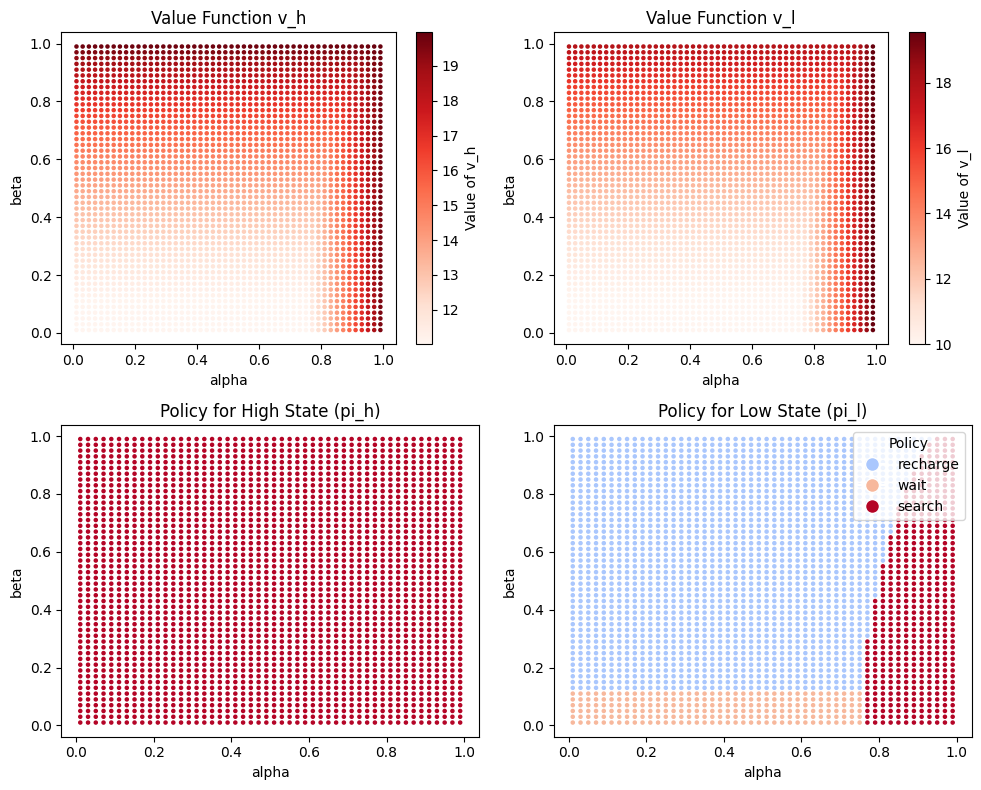Results of the linear programming solution Figure 1: Results of the linear programming solution.

References

  1. Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction (2nd ed.). MIT Press.

  2. Helmert, M., & Röger, G. (2021). Planning and Optimization: F2. Bellman Equation & Linear Programming.

Search